Right now the Monkeys write purely random, and mostly garbage, Z80 code which is fed into a genetic algorithm which then shapes it into something resembling a real solution to a problem.
There were several reasons why I wanted to add support for a real-world processor, even one that’s decades old, but a major one was so that I could somehow “train” the monkeys using existing Z80 snapshots, often referred to as ROMs. Large Language Models (LLMs) like ChatGPT are obviously all the rage at the moment but there are much simpler language models out there which we could build from scratch and “train” using the above ROMs. What if we create a new type of CodeGenerator that uses a simple language model to create programs that at least *somewhat* resemble real code, before feeding those into the genetic algorithm generators? Will that improve the efficiency of the system overall or have negligible impact? Will it make things *worse*?? Let’s find out…
Statistical Code Generator
We’ll create a new type of generator which we’ll call a Statistical Code Generator. This will replace the existing simple random generator in order to generate new solutions from scratch. In future I’ll refer to these as “Source Generators”, since they’re used purely to feed solutions into other generators.
The generator will use a simple N-Gram language model to generate the Z80 code. Check the link for more details, but this model is basically what you might find in a simple predictive text keyboard. Based on the previous N letters (or words), it chooses the next letter or word randomly based on the probability that this letter/word will appear next in the sequence. It’s far from perfect and it can’t write believable sentences like a large language model but it can still be useful for basic prediction.
In our case we’re not predicting letters or words but we can predict which opcode is likely to follow the previous N opcodes. For now we’ll just focus on the opcodes and continue to generate operands completely randomly.
Prep Work (The Boring Stuff)
If we want to analyze large amounts of code and run that analysis many times it makes sense to convert raw Z80 code into our 32-bit intermediate Instruction format and save that to a file so that we don’t need to decode it every time. Decoding is somewhat slow due to the variable length Z80 instructions and the different data formats for each instruction, as well as a dependence on other intermediate file formats, described later, that we’ll need to rely on in order to identify which parts of a ROM are actually code sections. For this decoding we need to perform the opposite of the encoding we did in the previous post, iterating through the Z80 binary and decoding the variable length instructions until the end of the data is reached. I made a long and tedious method to perform this, full of nested ifs and switch statements. It’s so very ugly that we’re not going to peek inside:
CodeGenerator::EncodingResult DecodeProgram(uint8_t* souceProgramMemory, Instruction::INSTRUCTION_TYPE* targetInstructions, uint16_t programSize, uint16_t programAddress, int& numInstructions);
Now we can encode and decode, but before we start delving into existing ROMs we’ll test the system using the the InstructionTest Exercise example which includes one copy of every possible Z80 opcode, and some duplicate copies of some of the opcodes for operand testing purposes. Here’s a snippet of that example:
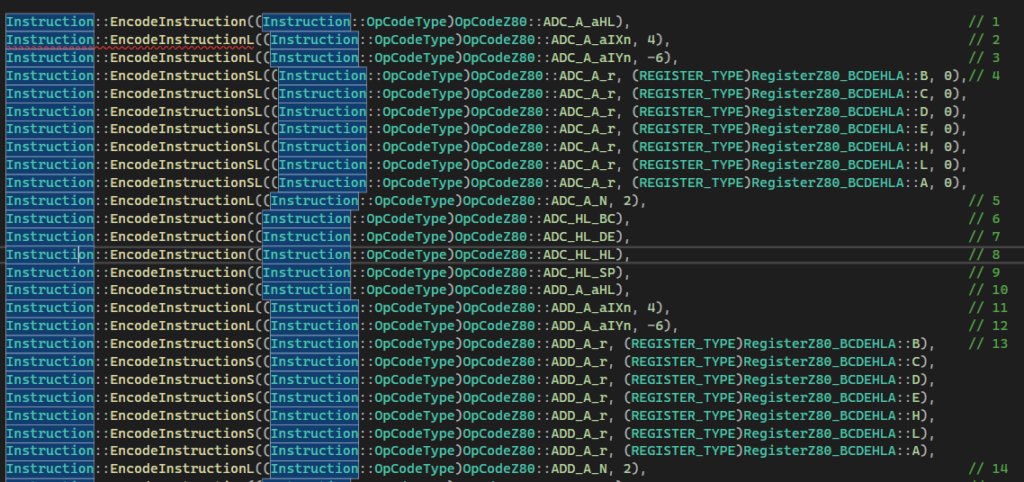
I created a test to encode the above example code into Z80 code, then decode it back and then compare the final result against the original example. Since every single instruction is included we can be pretty confident that the encoder and decoder are working correctly.
The intermediate code is saved into a .min (monkey instructions!) binary file which is just an array of 32 bit intermediate instructions, ready to be analyzed…
Unigram Number Generator
Now we have some test code to analyze we want to extract some stats. We’ll start with a basic Unigram language model which only considers the probability of an OpCode appearing anywhere in the code. Later we’ll advance to a Bigram model, which considers the previous OpCode in a sequence, and then try a Trigram model which takes the previous two OpCodes into consideration.
The process is pretty trivial, just load the .min program, iterate through each instruction and count the number of occurrences for each opcode. Then we dump that occurrence data out to another binary file (.opp) which will be used at runtime to populate our new generator. We use 16 bit values to count the number of occurrences for each of the 324 instructions, which results in a 648 byte binary file.
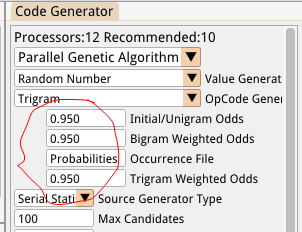
Now we can reuse the weighted number generator from Part 6 but this time we’ll populate it with the data from our new binary file instead of populating it dynamically at runtime. Since the weights are all known in advance we can use weighted sums and a binary search to more efficiently choose our random weighted opcodes. The C++ std::discrete_distribution essentially does this but I found it to be pretty slow and very memory intensive. It stores 16 bytes per weight, but we only need 4 for our weighted sums (and arguably even less than that). One we get into Trigram territory this would waste a pretty insane amount of memory. Instead I just wrote a custom C++ version of this which uses 4 bytes per opcode and performs a simple binary search on the weighted sums. It also removes the thread safety since we don’t require it (we have a unique random generator instance per thread). This number generator and the new Statistical Code Generator are now both exposed in the Code Generator setup panel:
Now we can test the system changes so far by:
- Analyzing the intermediate .min program, dumping the number of occurrences of each opcode out to an .opp file
- Loading them into our newly optimised number generator
- Requesting 100,000 samples from that class
- Tracking the distribution of values returned
We get the following distribution:
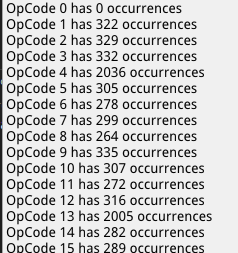
…and so on. OpCode 0 (Our ‘NONE/NULL’ instruction) has 0 occurrences because it’s not a real instruction, most opcodes have around 300 occurrences (100,000 / 324, roughly) and opcodes 4 (ADC_A_r) and 13 (ADD_A_r) have around 7 times that amount because they occur 7 times in the test program. Everything seems to be working properly, now we can finally delve into the real training!
Analyze Existing Code
We’ll analyze existing ROMs of Sinclair ZX Spectrum games to create more realistic weight data.
DISCLAIMER : All ROMs used are games that I’ve owned. The data created by analyzing them is only being used for testing purposes.
A ROM is mostly just a binary snapshot of memory and we don’t know which parts are comprised of code and which are data. We need a way to figure out where the code lives.
I took advice from this great source of information, tweaked it a bit and came up with the following process to extract the actual code:
- Use .rzx files instead of a regular snapshot. These contain not just the memory snapshot but also a bunch of replay data. This replay can be performed inside an emulator instead of having to play through the game manually. This site has an amazing collection of full playthroughs of many Spectrum games.
- Load the rzx file into the Fuse emulator, export a copy of the snapshot in .szx format for use below and start the profiler. The replay will be replayed and the profiler will store information on which instructions have been executed at specific memory addresses.
- Once the replay is complete, stop the emulator and save out the generated .map file.
- Use SkoolKit to create a .skool and .bin file from the saved .szx and .map files. The .skool file contains an analysis of the ROM, breaking it down into various sections (ie. code and data).
- Write a custom tool to read the .skool and .bin files and decode the raw Z80 code into our intermediate Instruction format, then dump that out into a .min file as mentioned earlier.
- Eyeball the output from the previous step to discard any programs which seem to contain erroneous data. This can happen if, for example, a section of code memory was overwritten at runtime to be reused as a data section of memory.
- Load the .min file, analyse it and dump out the probability .opp file
Repeat this for every single ROM and we’ll have a nice collection of data to play with.
Code Analyser Panel
I created this Code Analyser panel to help automate some of the above processes:
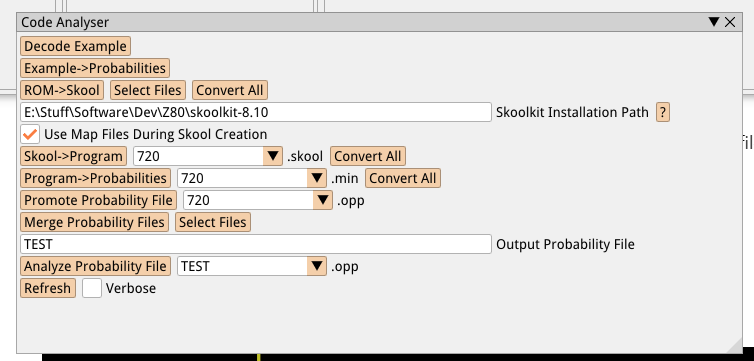
It has some basic utilities to test the decoding we talked about earlier, but it can also batch process certain steps, such as the conversion from ROM+map files to skool files, converting those to programs and creating .opp files from each program. Finally, it can merge all .opp files into a single set of probabilities which will be used at runtime by the generators.
Training
I used the replay feature to blast through the games as quickly as possible. It was a loooong and pretty tedious process but it was at least fun to see the endings of some of the games that were far to difficult to beat back in the day, and obviously I had to play some of the games manually for my own sanity and the sheer nostalgia factor:

ROMs were only included if I had owned the game, if they were 48k versions (128k were rejected because I didn’t want to figure out memory paging issues yet) and if the final decoded instructions they produced appeared to be valid.
Numbers, So Many Numbers
In total we successfully analyzed 263 ROMs.
From that we extracted 1,225,201 instructions
Out of 323 opcodes, 306 appeared at least once within that entire set of data. 17 are never used.
The most commonly used opcodes?
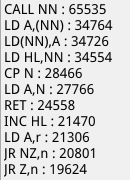
Those which didn’t make an appearance (note that NONE isn’t a real opcode):

I shared this data with the Z80 Assembly Programming On The ZX Spectrum group on facebook where smarter people than I were kind enough to confirm that these values appear to make sense. The data might not be perfect but it certainly looks useable.
Unigram
As an initial test, let’s see if the Unigram generator can solve the “Sequence of 8 numbers” Exercise without using the genetic algorithm generator at all. Can it just spit out a program which works? The old random generator couldn’t…
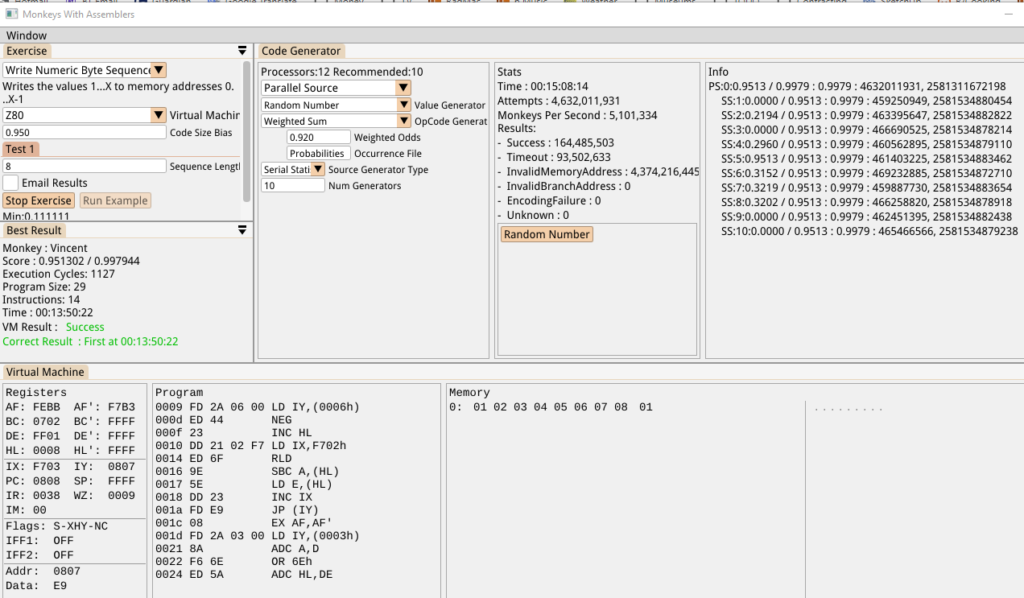
Yes, it can! In just under 14 minutes in this case. The code is….just…awful, but it’s surprising that it strung together a program of 14 instructions which solves the exercise *and* executes successfully.
Bigram
Next we add Bigram support. For this we need to know the odds of each opcode occurring after every other opcode.
In terms of analyzing and saving the opp data, it’s implemented as a 2D array, simply NumOpcodes * NumOpCodes (in our Z80 case, that’s 324*324). With 2 byte probabilities the data uses 209,952 bytes on disk.
We index it using:
index = (n1OpCode * numOpCodes) + currentOpCode;
Where n1OpCode is the previous opcode in the sequence.
At runtime we basically create a separate weighted sum generator for every single n1 opcode and populate it using the relevant section of this data. We also create a unigram generator for picking the initial opcode in a block of code and another one for picking an opcode when it’s determined that the bigram generator shouldn’t be used (controlled via a tweakable setting that lets us specify how much influence the bigram generator has).
Trigram
The Trigram solution is similar to the Bigram one but adds another dimension to the array:
Data size = NumOpcodes * NumOpCodes * NumOpCodes * 2 bytes = 68,024,448 bytes on disk.
index = (n1OpCode * (numOpCodes*numOpCodes)) + (n2OpCode * numOpCodes) + opCode;
n1 refers to the previous instruction, n2 refers to the instruction before that, so we’re now considering sequences of 3 instructions (hence the trigram name!).
Here’s a comparison of the different levels of code generation, from our original 100% random version to the trigram version.
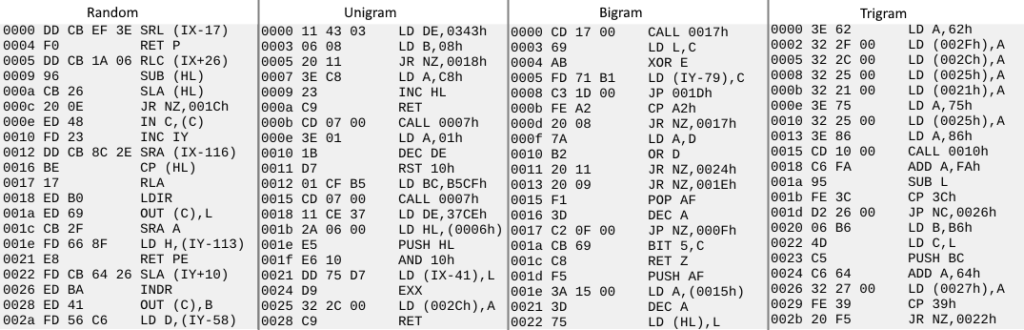
- The random version contains a few IO instructions (IN, OUT, INDR) which aren’t used all that much unless you’re writing software that’s very IO intensive. We don’t see any pairing of instructions either, since there’s zero context when choosing the next instruction.
- The unigram code looks a little more like code. It only considers the likelihood of an opcode being used, so the main benefit is to strip out the less frequently used instructions.
- The bigram version also strips those instructions but the code appears to have some pairing of instructions too. For example, loading the A register and then performing an operation on it, or pushing the same register before operating on it. This is because each instruction is chosen based on the likelihood of it following the previous instruction in real code. It still doesn’t look much like useful code though.
- The trigram takes it a step further by considering the two previous instructions. The first 10 instructions actually seem like valid code, using the accumulator to set a bunch of values in memory before calling a subroutine which we could imagine would then use those values. Other combinations of instructions look ‘correct’ too, such as the loading of the B and C registers before pushing both on the stack or the conditional branch after a comparison.
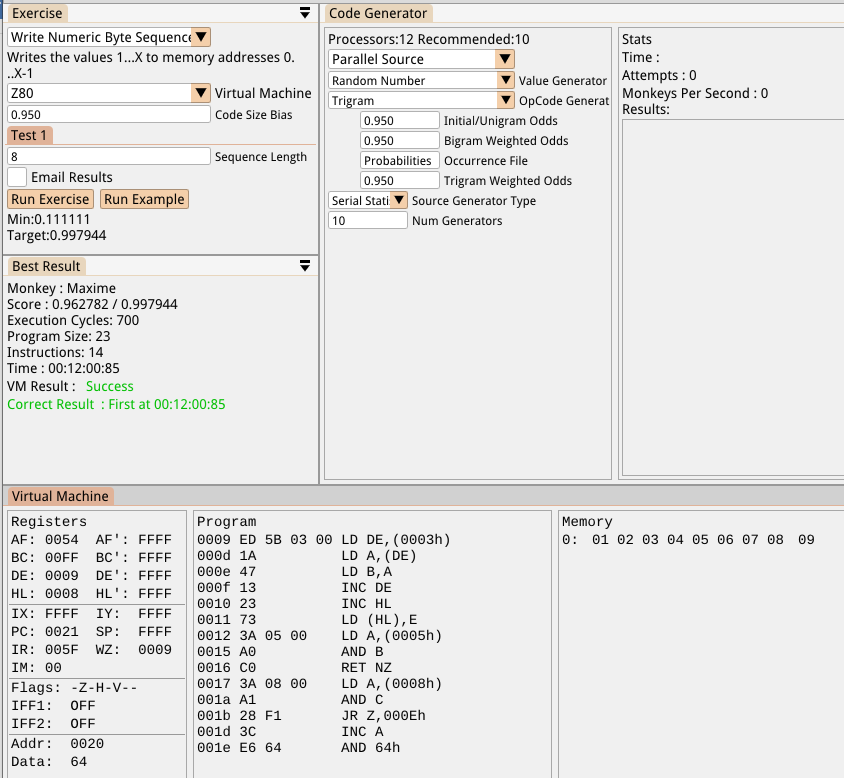
Repeating the previous test using just the trigram generators, the monkeys can complete the “Sequence of 8 numbers” without the GA generator in slightly less time and with much less ridiculous looking code:
Copy String
In the last post we saw that the monkeys failed to find a solution to the “Copy Char String” exercise because they weren’t able to find a way to utilize the null string terminator. We’ll try this again using the Trigram+genetic algorithm generator combination.
This time, to make it harder for them to write hacky solutions, we’ve added a 3rd Test to the Exercise which just requires them to copy the word “Hi”, in addition to the previous Hello World!, Bonjour Tout le Monde!:

Just to confirm, we’ll test with the old random generator first. As expected, the previous optimal setup still couldn’t solve this, even given 16 hours. It’s just never able to produce a loop:
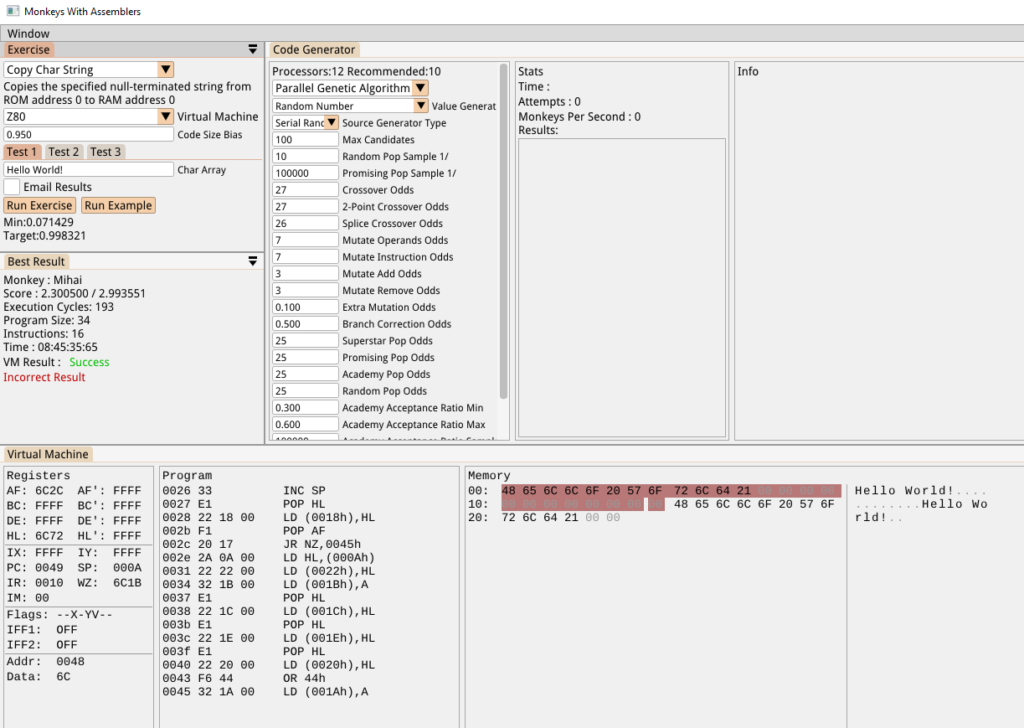
Using the bigram generator as a source gave us a successful result:
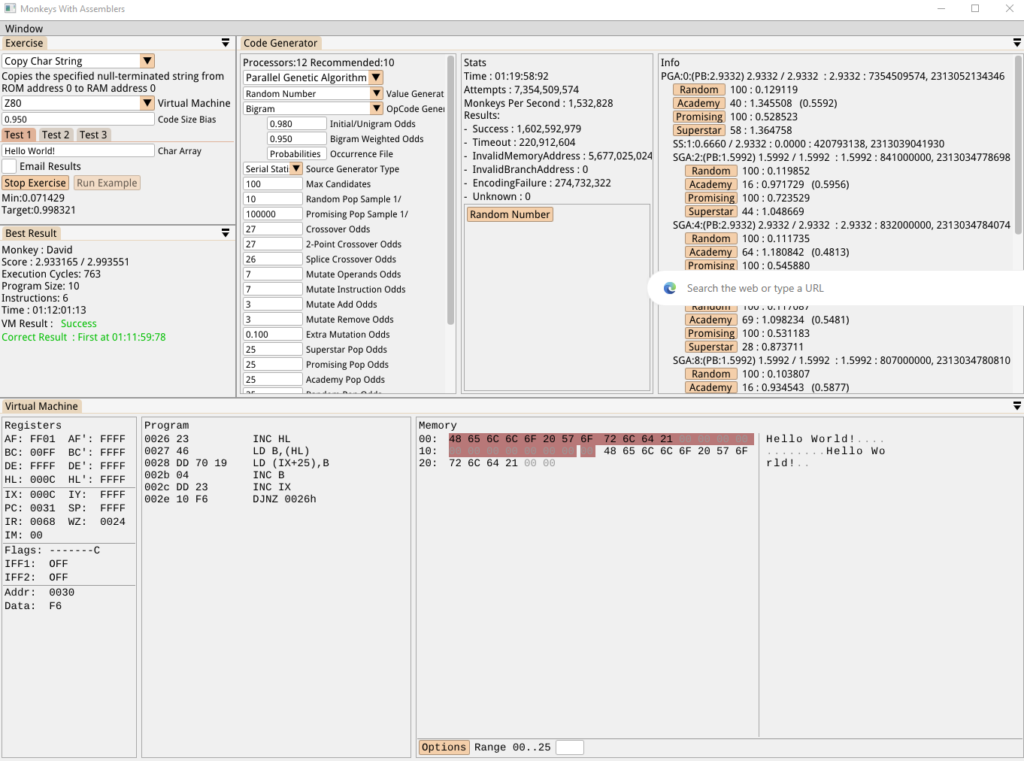
Hurrah! And here’s the Trigram generator, taking just over an hour:
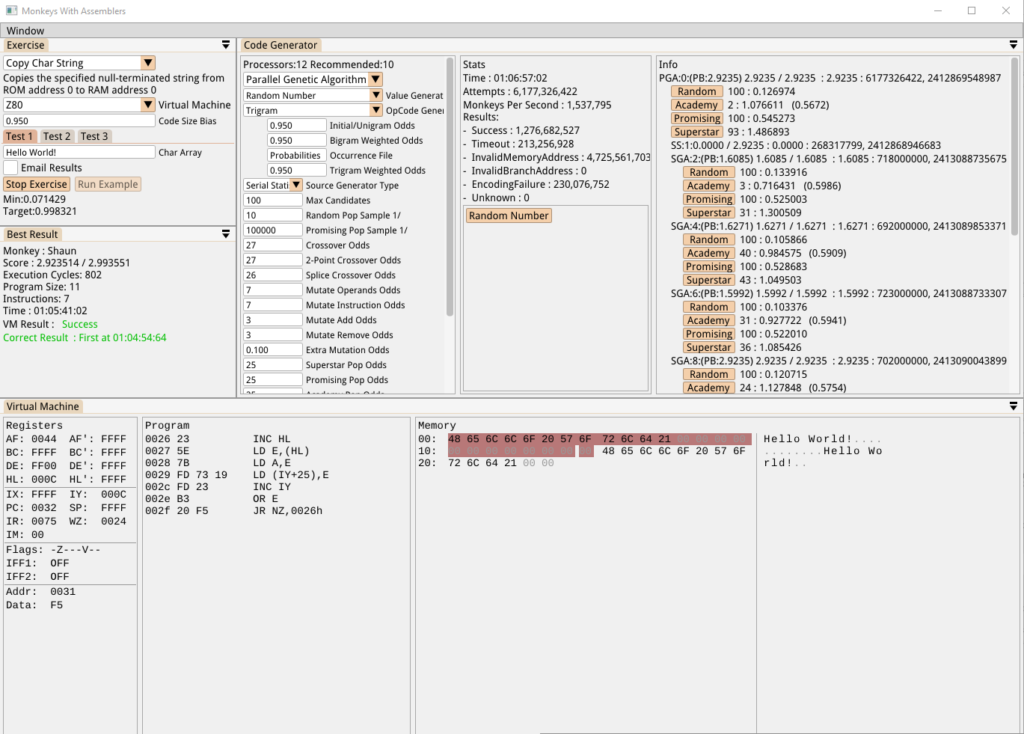
But the next identical attempt gave us this:
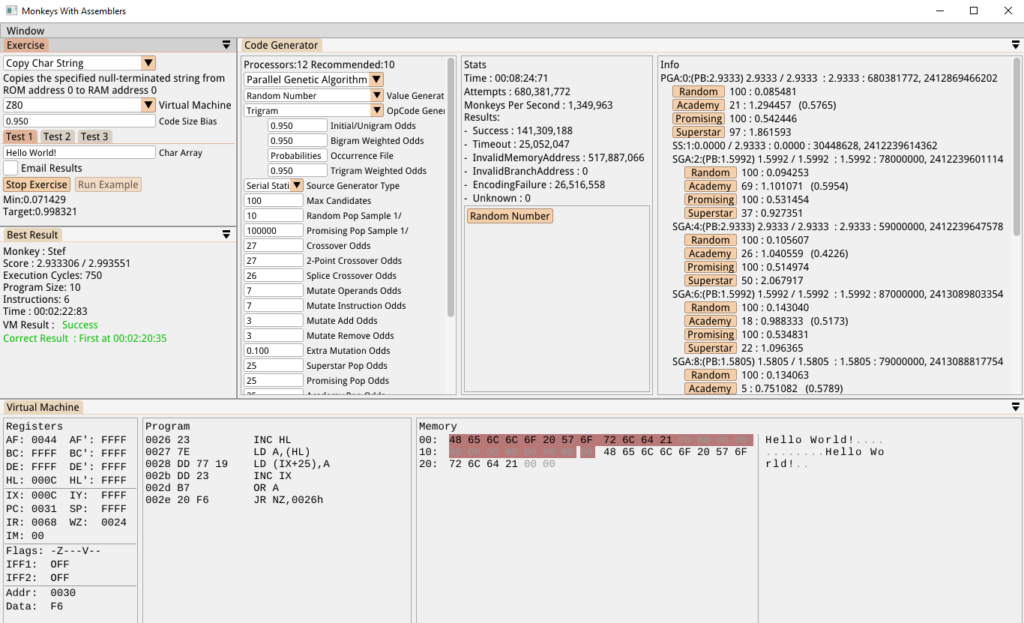
…in less than 3 minutes. This is a huge improvement! Here’s a recording of another attempt that took just 31 seconds, including a description of what’s actually happening:
Star Exercise
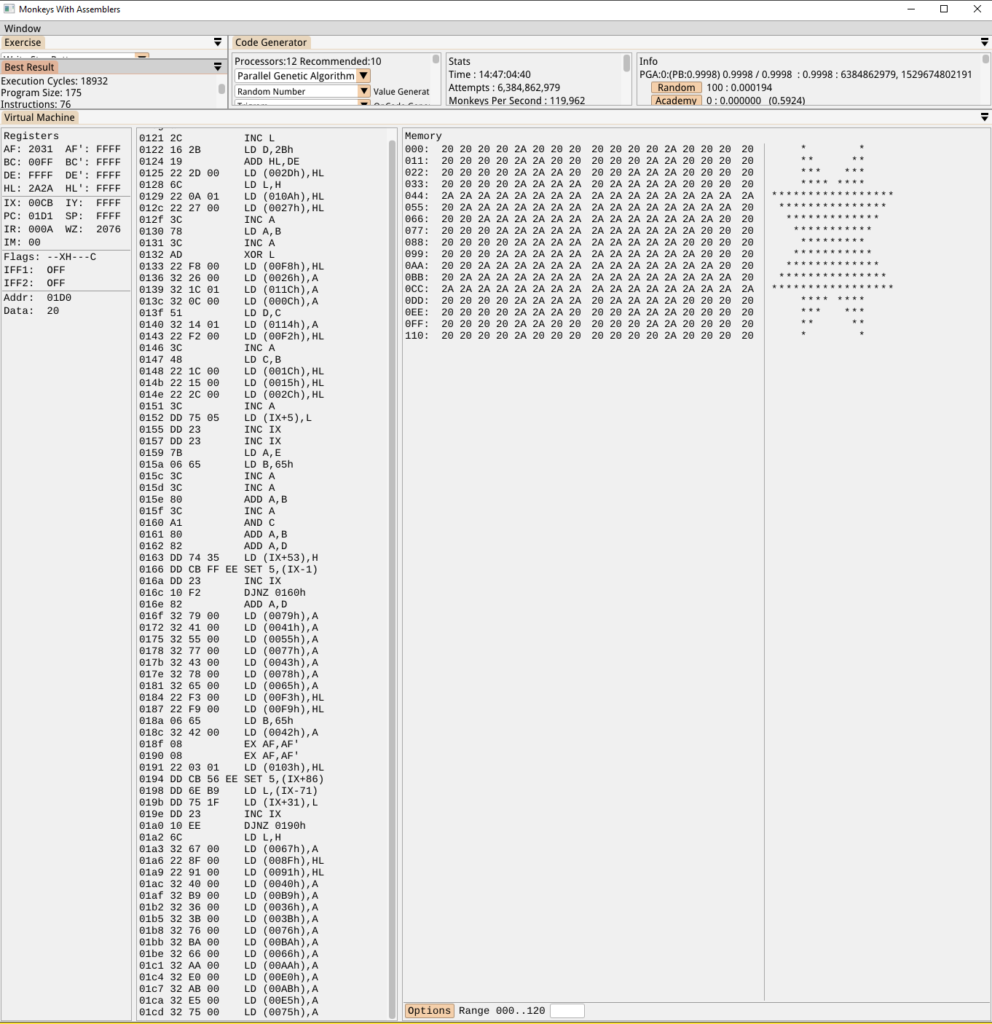
I always like seeing how the monkeys approach the star exercise. I set it to focus on minimal code size and the solution took just 76 instructions to write a pattern of 289 bytes. That seems somewhat efficient in terms of code size but is understandably much less efficient in terms of performance. It’s interesting to see how it’s relying on the IX register throughout the program:
Conclusion
The new n-gram generator doesn’t perform miracles. It’s a simple language model built on a relatively simple set of data. That said, it *did* allow the monkeys to finally write that string copy loop in a reasonable amount of time, something that was previously impossible. It’s definitely going to be a useful tool in the arsenal and is something we can build upon in future. Right now we’re using this just to predict opcodes, but we can pull all kinds of useful info from the training data. For example, we could build sets of weights wherever constants are used. We might find that 0 and 1 are loaded into registers far more frequently than, say, 78, and could use this data when generating operands for an instruction. The same goes for the choice of register or memory address. This would build on the not-so-successful number generator approach we added in part 6.
We could also weight opcodes based on their location in the code. For example, PUSH instructions might be more likely to appear at the start of a block of code, and RET instructions at the end. There’s a lot of potential here, I think.
I suppose one negative aspect of this whole approach is that it perhaps coerces the system to code like a human would and potentially prevents it from finding more efficient, novel solutions that might not be obvious to a regular programmer. Hopefully we avoid this by using the settings that allow the system to fall back to a fully random selection:
What’s Next?
I had to create a Trello project to track all the ideas I want to work on next. There’s the expansion of this language model to include operand selection, or finding a way to back out of evolutionary dead-ends, or improving the configuration of each code and number generator so that we can set up a more interesting graph of generators, or adding support for parameter passing in the generated code, or giving the monkeys the ability to create data sections as well as code sections, or adding a new, more complex exercise to give us a new challenge to beat. We’ll see.
“Why Don’t You Just Use ChatGPT??”
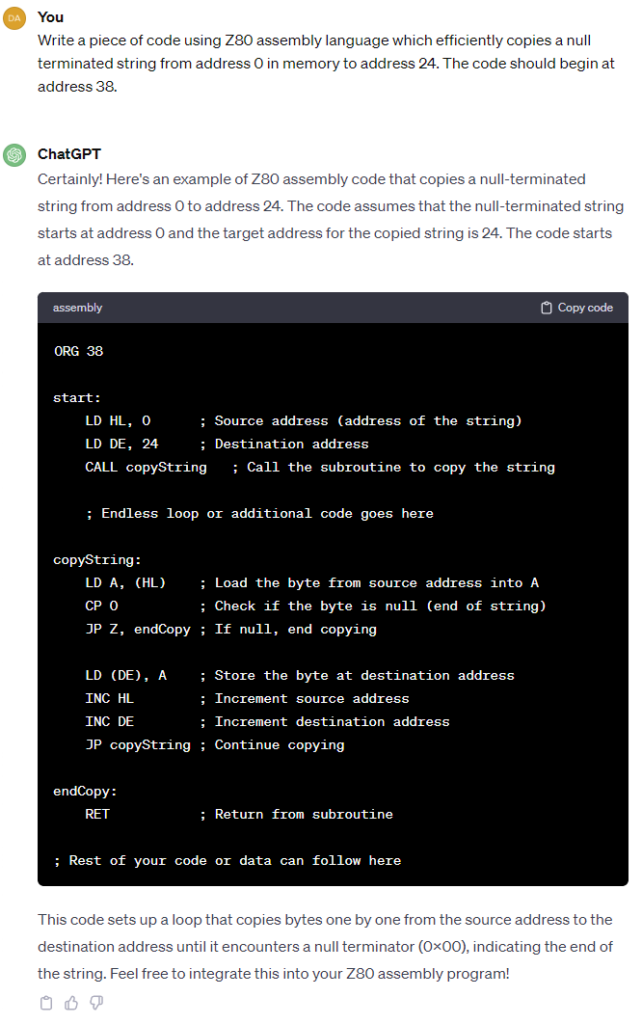
Since we’re looking at language models I figured it would be fun to ask ChatGPT 3.5 to try to solve the same string copy exercise we finally solved above:
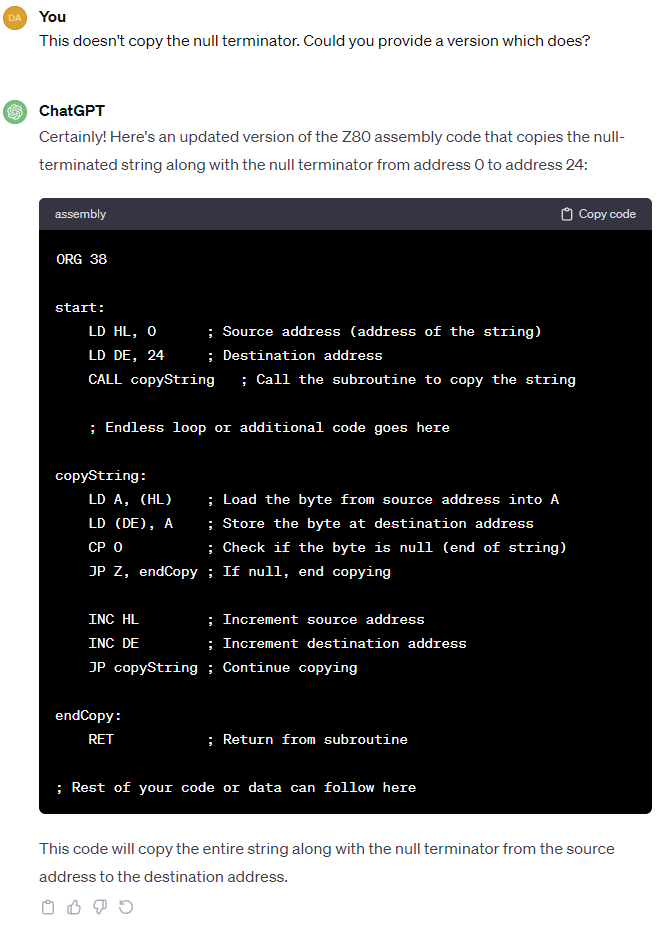
To be fair here, ChatGPT is relying on the stack pointer being correctly initialised, and I didn’t state that it shouldn’t use a subroutine. Let’s see if it can correct that…
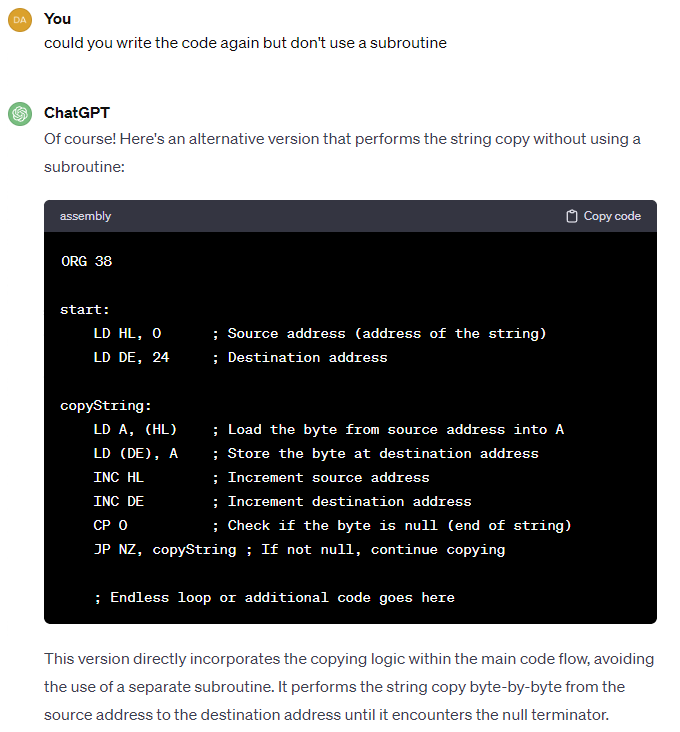
Yep, that’s a good response! It’s pretty impressive, really. If I use this as the example code in the Exercise I get this:
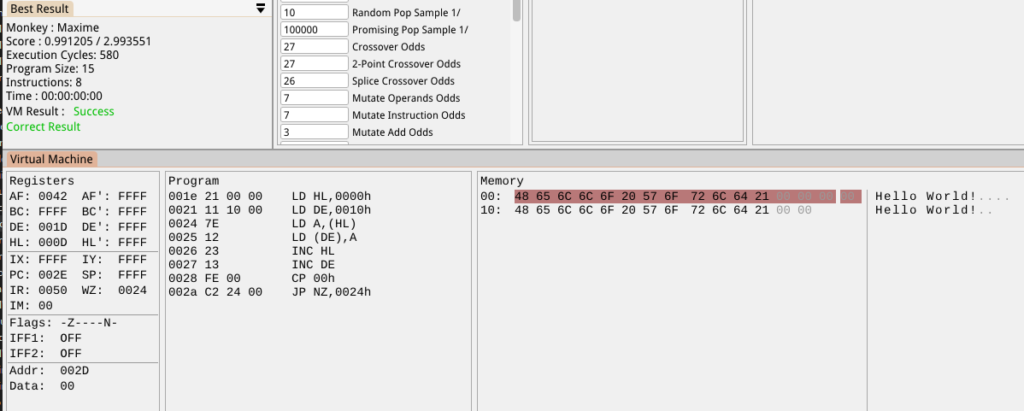
It’s less efficient than the most efficient monkey version I’ve seen. That code was 437 cycles (vs 580), 10 bytes program size (vs 15) and 7 instructions (vs 8). I wonder what ChatGPT thinks of this?

Pshhh! Excuses, excuses….
’til next time!