This Monkey’s Gone To Seven

We left our monkeys with the ability to count to 3 in a mere 20 minutes. I’m proud of them but it’s not going to earn them any bananas.

The next step is to count to 8. I think this is the tipping point at which a loop will be more efficient in terms of code size than just raw load/stores and I’d like to see if they can consistently produce working conditional loops. It will, however, be less efficient in terms of instructions executed, so I tweaked the exercise evaluator to favour smaller program size over instruction execution count. The first attempt looks like this:

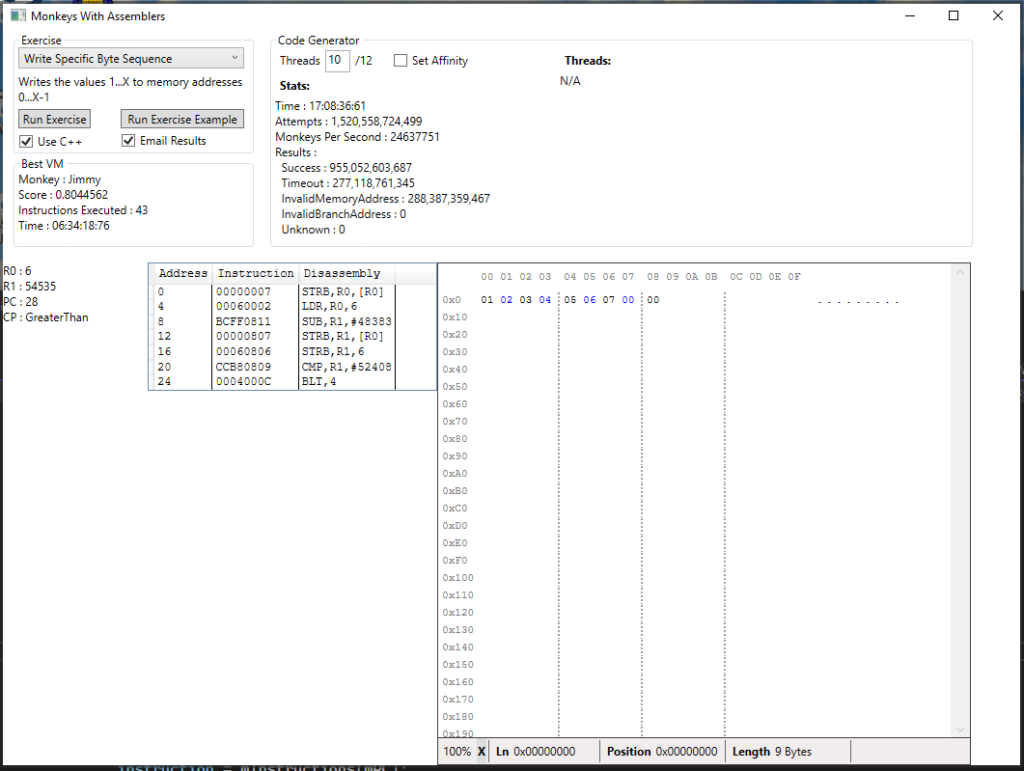
After 17 hours they hadn’t found a solution, only managing to count to 7. I sent the monkeys home at this point because they were just wasting electricity.

Then I started looking at some of the erroneous solutions and seeing minor errors that could be tweaked to make the solutions more accurate, perhaps by pruning or tweaking instructions or modifying operands. Then someone pointed out that I’m basically re-inventing genetic algorithms, so I did some reading on the topic and, by jove, they’re right!

I think we can take the basic concepts of GAs and adapt them to create a new type of code generator which will take our randomly generated programs and modify them in an iterative way until they become valid solutions.

First, it’s time for some cleanup so I spent some time:

• Adding proper support for multiple generators. I made all generators derive from a base CodeGenerator class, and we can choose which of these generators to use via the UI:
  • SerialRandomCodeGenerator : Generates random programs until a target score is met
  • ParallelRandomCodeGenerator : Creates and manages X SerialRandomCodeGenerators, keeping track of the best result until a target score is met
  • GeneticAlgorithmCodeGenerator : Our new generator which will use a ParallelRandomCodeGenerator to provide a stream of completely new, random programs, then runs its own generation routine which applies genetic operators to those programs
• Adding a parameter system to more easily expose parameters from the generators and exercises in the UI
• Evaluating failed solutions and doing some cleanup on invalid instructions:
  • Don’t allow a branch to the next instruction, it’s completely useless
  • Don’t Load or Move to the same register that has just been modified (by a load, move, add or subtract). Doing so will just override results of previous operations and renders them useless

Genetic Algorithm Code Generator

As mentioned above, the genetic algorithm code generator is a completely separate generator which will be fed input from the existing parallel random generator, apply ‘operators’ to those solutions and store the results in a population of some sort. We’ll repeat the process on that population until an optimal solution is found.

Genetic algorithms have some kind of ‘fitness function’ which determines how ‘fit’ a solution is, which then affects its role in the population. For example, when do we discard the solution? How likely is it to be selected for future iterations? Our Exercise score is already essentially a fitness function, so the existing code translates perfectly to this approach.

Then we need some operators, so what should they look like?

Mutation Operators

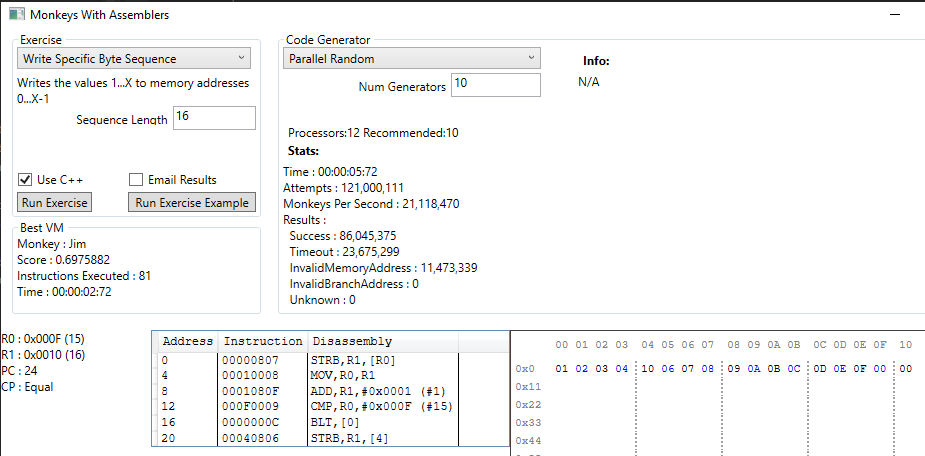
In the above example we tried to create a sequence of 16 numbers.

Note : For this test, out of curiosity, I limited the range of random constants we can choose for operands to 0-16, instead of 0-65535, just to see if a valid solution could be found.

Jim did a pretty good job of writing a sequence of 15 characters, but we wanted 16. In this case, mutation of the CMP instruction could fix the problem by modifying that constant to the correct value. That mutation would be far more likely to occur than randomly generating this entire program again with a different value.
There’s also a rogue ‘STRB’ at the end of the program which is trashing the sequence. This would be fixed through truncation by randomly snipping instructions from this program.

So, we’ll start by adding four basic operators which will be used to create new children:

• Mutate Instruction : From a single parent, replace an entire instruction and its operands with a new instruction
• Mutate Operands : From a single parent, replace the operands of a single instruction with new operands
• Add/Remove Instruction : From a single parent, add or remove a single instruction chosen from a random location in its program

The children of these mutations will be evaluated in the same way as the random solutions. Any solution that beats a certain score threshold will be added to the population and can be chosen for future mutations.

Our First Baby Monkeys

For the first test, we’ll:

• Maintain a simple population in our new generator. For now we’ll specify a maximum population size and just remove the oldest member once the capacity is reached.
• Periodically add some random monkeys to the population from the Parallel Random Generator.
• Choose a random program from the population
• Randomly choose and then apply a mutation operator to that program
• Score the result using the existing Exercise scoring method
• Store the resulting program in the population if it beats our high score

Let’s mutate!

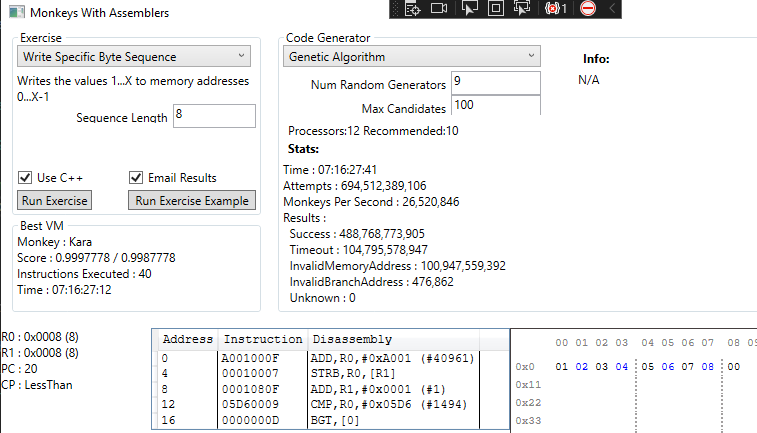
Previously the monkeys had failed to solve this, I’d cancelled them at 1.5 trillion attempts. Now they found a solution. It still took over 7 hours and nearly 700 million attempts but we got there.

With the current setup, it appears that the mutations are only really effective when an almost-working random solution has been provided. Using that they’ll quickly fix any incorrect operands and trim unnecessary instructions. Below we can see an example of this occurring in a very short space of time. First a MUTATE_REMOVE operator randomly removes the unnecessary END instruction, then a MUTATE_OPERANDS operator modifies the value used by the CMP instruction to fix our weird little loop, with the score improving with each mutation.

Score : 0.8533334 Time : 00:16:19:63 Program :   0 : LDR,R0,[7]   4 : ADD,R1,#0xB501 (#46337)   8 : STRB,R1,[R0]   12 : STRB,R1,[7]   16 : CMP,R1,#0xEB8E (#60302)   20 : BLT,[0]   24 : END Memory: 01 02 03 04 05 06 07 07 00

Score : 0.8687778 Time : 00:16:19:63 Program :   0 : LDR,R0,[7]   4 : ADD,R1,#0xB501 (#46337)   8 : STRB,R1,[R0]   12 : STRB,R1,[7]   16 : CMP,R1,#0xEB8E (#60302)   20 : BLT,[0] Memory: 01 02 03 04 05 06 07 07 00

Score : 0.9532222 Time : 00:16:19:73 Program :   0 : LDR,R0,[7]   4 : ADD,R1,#0xB501 (#46337)   8 : STRB,R1,[R0]   12 : STRB,R1,[7]   16 : CMP,R0,#0x0007 (#7)   20 : BLT,[0] Memory: 01 02 03 04 05 06 07 08 00

As we get closer to our target score, these almost-correct random solutions take a long time to generate and we’re relying too heavily on the random generator again. I think we can fix that with a couple of additions: a crossover operator and improvements to the selection of parents from the population.

Crossover Operator

The crossover is pretty standard genetic operator which combines data from 2 or more parents to produce a child. In our case, we’ll add a simple crossover operator to our existing mutation operators. This will take two random parents, pick a crossover point and combine the initial X instructions of parent A with the last Y instructions from parent B to produce a child.

Selection

For the first test we were just storing a population of the most successful solutions so far. In some cases this gets us to a solution really quickly but it can also drive us very quickly down an evolutionary dead-end.

For the next attempt we’ll track 3 separate populations:

• Superstar Monkeys – A collection of solutions that managed to beat the current high-score, regardless of the source of those solutions (crossover, mutation, purely random). We’ll assume that *something* in each of these solutions is likely to be valuable and, for now, will never remove any members from the population
• Promising Monkeys – A collection of solutions that matched or almost reached the most recent high score. Initially, we’ll prune the oldest monkeys in this population to keep it at a manageable size.
• Random Monkeys – A random selection of monkeys populated by the results of the random code generator. Score won’t be considered. The population will be refreshed periodically. These monkeys will bring fresh blood to the entire population and hopefully steer us away from dead-ends.

We’ll also use the new parameter system to expose the odds of selecting a candidate from each population and the odds of selecting a particular genetic operator on each iteration, which lets us easily experiment with different settings.

Below is an attempt to solve the sequence of 8 using the new population code:

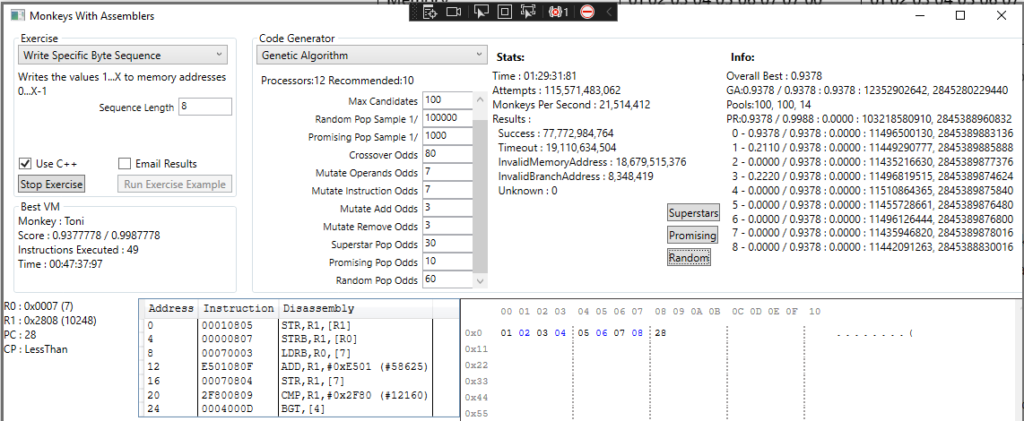
It was failing to progress past this point and I ended up cancelling the test.

It At First You Don’t Succeed, Keep Failing Miserably

After experimenting with different values for a while, the monkeys still couldn’t solve the exercise efficiently.

I added buttons which allow us to view the members of the current population groups. In this case we can see that lots of near identical ‘Remove’ mutations are swamping the Promising pool:

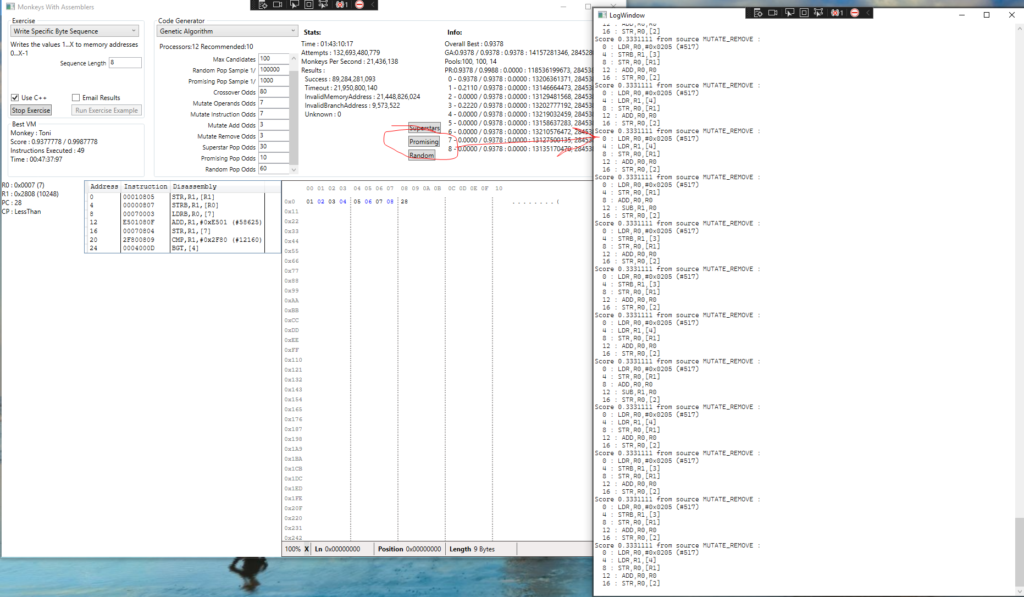
How do we prevent this? There are a lot of things to experiment with, particularly the management of these population groups. Which solutions should we keep? Which should we purge? How large should the population be? How do we ensure that fresh blood can have an impact on the population if it doesn’t immediately produce high scoring solutions? eg. How do we promote looping code over brute force load/stores without explicitly telling the monkeys what to do?

Let’s try some small tweaks first:

• Add concept of a ‘Minimum score’ to the Exercise. This will typically be the lowest score possible that actually indicates progress towards the solution. eg. the score given when one number in a sequence has been set correctly. This could be useful when determining whether to add a monkey to a particular population.
• As the superstar population grows, prune monkeys below the minimum score. They’re probably only there because they were created early and managed not to crash, but don’t really offer anything useful

I tried the above and it didn’t really improve anything. I played around with some other ideas too. Adding a unique ID to each solution and tracking information about its parent(s) meant that I could only consider them for the POTENTIAL population if they scored higher than their parents, or make sure that we can’t have too many equal scoring children from the same parents.

None of this solved the problem above and actually just made it even harder to find a solution, as well as negatively affecting performance due to the cost of managing the populations.

So I rolled things back a bit and took a different approach…

Loser Monkeys

What about all of the monkeys that created erroneous solutions, either by accessing or branching to an invalid memory address, or by breaking the instruction execution limit, essentially timing out?

Surely these solutions are useful? What about a perfect loop that just happens to iterate too many times? Or a solid solution which just happens to have an invalid store instruction thrown in? It made sense to discard these in the random generator when we had no way of fixing them, but now they could be useful additions to the population.

So, I tried allowing erroneous solutions to be reported in the same manner as successful ones.

Surprisingly, many of the erroneous results were scoring remarkably high and quickly flooding the promising pool, so it required some more restrictions:

• An erroneous solution cannot be added to the Superstar population.
• An erroneous solution can only be added to the Promising population if it beat the scores of its parents or if it’s randomly generated and matches the current best score.

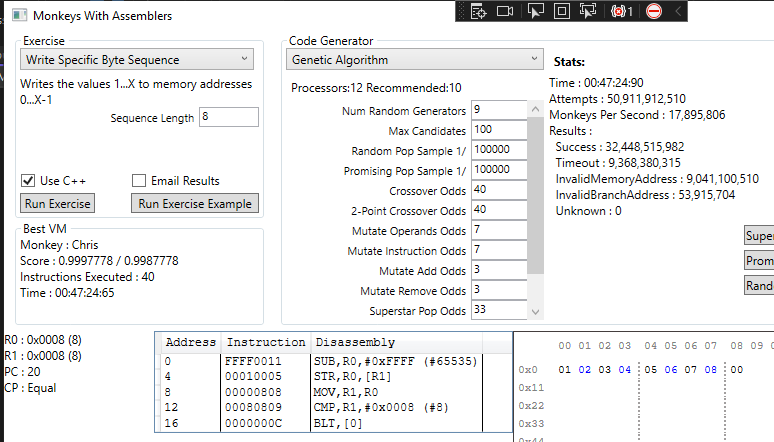
Et voila! Finally, we’re able to generate the optimal loop for a sequence of 8 in 47 minutes. Good work, Chris the Monkey!

Monkey Academy

Next, we need a way to foster a diverse population to avoid the evolutionary dead-ends mentioned above. Diversity seems to be an important concept in genetic algorithms and it’s definitely something we’ve been lacking so far. We have the fully random solutions which are, of course, incredibly diverse, but they’re not given much opportunity to evolve before being banished from the population.

I think they need a place to flourish independently, so let’s add the concept of an ‘Academy’ population.
This will be similar to the Promising population but will not accept any Superstar descendants. We want the academy to feed into the Promising and Superstar pools but not the other way round. I had to play around with the rules but settled on these entry requirements:

• Monkey must not be a Superstar descendent (prevent elites from dominating this population)
• Monkey must not be a child of a Promising parent. (similar to above)
• Monkey must have executed a successful program, or one of its parents must have executed a successful program (to prevent multiple generations of errors from flooding the population)
• Monkey must beat their parent score (if it has parents) and 50% of the current high score (to weed out low scoring monkeys but still allow room for growth)

Also, whenever a new Superstar member is created we’ll destroy the Academy population. If an academy member becomes a Superstar we don’t want their fellow Academy members to flood the academy with imitations. That could potentially lead us down the same evolutionary dead-end we were seeing before.

With a bit of tweaking, it works, and it works surprisingly well! We got an optimal solution in 27 seconds!

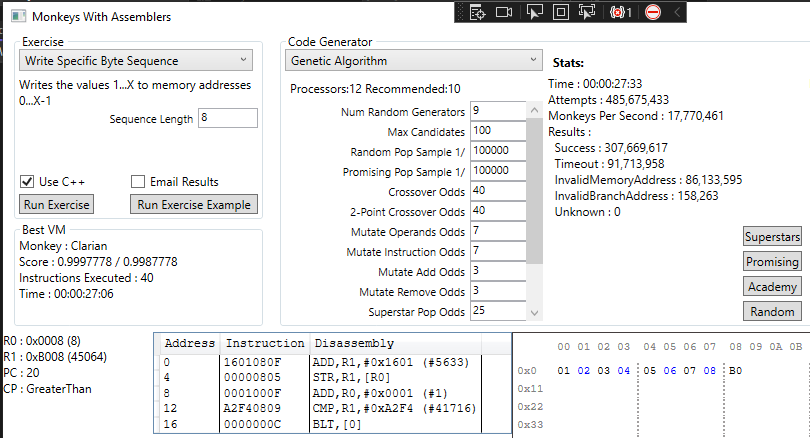
Next, I tweaked the academy admittance criteria to only require 25% of the current high score and this happened:

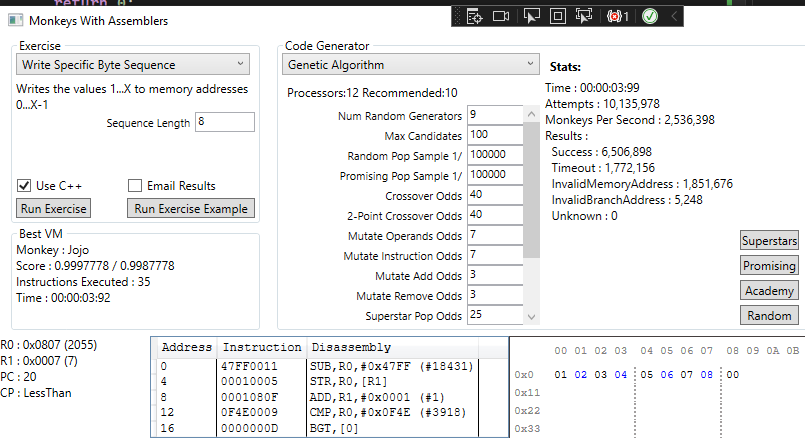
It took less than 4 seconds to find a result but, more surprisingly, it found a way to shave another 5 instruction cycles off the solution. Way to go, Jojo!

I should add a disclaimer that these timings are definitely not consistent due to the random nature of our generators. At this point we’re probably averaging around 2 – 3 minutes to find a 40 cycle solution, which is still amazing progress compared to the failed 17+ hour attempt we started with.

Monkey Magic

I think at this point we can say that the monkeys are capable of creating a conditional loop, which is what we set out to achieve. I’m pretty satisfied with the progress so far and, overall, I see a lot of potential in this genetic/evolutionary approach. We could play with operators, populations and selection techniques for weeks and perhaps find a subsecond solution, but for now I’m really, really tired of watching monkeys breed and fancy a bit of a change.

Star Pattern

Speaking of change, back during the the holidays a vintage computing group put out a challenge to create a minimalist program that generates a 17×17 ‘Christmas star’. I thought it’d be fun to let the monkeys have a try using a much earlier version of the genetic algorithm generator. They actually succeeded, in a clunky kind of way, and I find it weirdly therapeutic to watch. Here they are in action:

What’s Next?

There are a few improvements and optimisations I was hoping to try soon. To challenge the monkeys we’ll create some more complex Exercises that’ll require them to work smarter, so we’ll need those improvements.
Hopefully they’ll succeed, I’m starting to have faith in my hairy friends!